#043 - Computational Design in the Built Environment: The Power of Bayesian Methods
Leveraging Bayesian Methods in Computational Design: Practical Tools for Informed Engineering Decisions
In engineering, decision-making often involves navigating complex systems under uncertainty. Traditional approaches rely on deterministic models and conservative estimates, which can lead to over-engineering or unanticipated risks.
"It is a capital mistake to theorize before one has data. Insensibly one begins to twist facts to suit theories, instead of theories to suit facts."
- Sherlock Holmes
As computational design tools become increasingly integrated into engineering workflows, data-driven methods become more useful.
Bayesian methods, with their ability to update predictions as new data becomes available, offer a practical solution for making informed decisions.1
This article explores the role of Bayesian methods in infrastructure design and highlights the importance of using these tools to enhance decision-making without requiring deep mathematical expertise.
I will provide a couple of examples in Python to illustrate concepts. You knew this was coming.
Maybe this sounds both dry and difficult. It’s not. You can use these tools in so many engineering applications and you will be surprised how easy it is.
We all use Google Maps but most us have no idea how Google Maps actually works, so bear with me.
Effective engineering relies on the efficient use of available tools.
Most governing design codes do not explicitly explore Bayesian methods2, instead leaning heavily on deterministic approaches and historical data or research.
As engineers, we have a professional responsibility to adhere to these codes where relevant. However, experienced engineers recognize that there are many grey areas in design and analysis that require professional judgment, and often, these are high-stakes decisions.
This is where Bayesian methods offer significant advantages—allowing us to incorporate uncertainty, update assessments with new information, and make more informed decisions. By doing so, we not only enhance our own decision-making capabilities but also provide better outcomes for asset owners, construction companies, the public and the environment.
The Role of Computational Design in the Built Environment
Computational design is the norm in most major infrastructure projects. It provides engineers with advanced tools for modelling, analysis, and optimization, allowing them to manage the inherent complexity of infrastructure systems.
In all projects, engineers face uncertainties, things like material properties, environmental conditions, constructability issues or data gaps. Traditional methods often address these uncertainties through conservative assumptions, which can result in either excessive and costly safety margins or, even worse, unexpected failures.
We address these challenges by integrating tools like finite element analysis, optimization algorithms, simulation techniques and professional judgment.
However, the value of computational design is realized only when the data generated by these tools is interpreted and applied correctly. Bayesian methods provide a framework for managing uncertainty and making informed decisions, offering a practical solution to the limitations of traditional approaches.
While data-driven engineering is currently in its infancy, we are on the path to more and more data collection, management and informed utilization. We are moving away from the calculation of isolated project components to analyzing and building our projects as a complex system of moving parts and evolving variables.
It’s helpful to understand the topology of this landscape.
Introduction to Bayesian Methods
Bayesian methods are a set of statistical techniques grounded in Bayes' Theorem, which offers a logical process for updating the probability of a hypothesis as new evidence becomes available. In engineering, Bayesian methods improve decision-making by incorporating prior knowledge and updating predictions as new data is collected.
The fundamental concept of the Bayesian method is about updating our beliefs with new information. When we receive new data or evidence, we combine this with what we already know to form a new, updated belief.
This process helps us make better decisions or predictions because we're continuously refining our understanding as more information becomes available.

For example, Bayesian methods in fatigue analysis allow asset owners, such as highway and transport agencies, to dynamically update estimates of a structure's remaining life by incorporating new inspection data with prior knowledge. This approach enables more informed decisions about maintenance and safety, optimizing resource allocation and preventing unexpected failures. By continuously refining their understanding of a structure's condition, agencies can proactively manage infrastructure, ensuring long-term reliability and cost-effectiveness.
Bayesian methods are similar to machine learning models in their ability to handle uncertainty and continuously refine predictions by incorporating new data. Bayesian methods do this explicitly by updating probability distributions, while machine learning models often do this through iterative optimization processes.
Some machine learning models are considered "black boxes" that prioritize predictive accuracy, especially in applications requiring large datasets (e.g., YouTube algorithms, social media). However, these models struggle with interpretability and are less effective with small or noisy datasets. This limitation makes some machine learning models less suitable for certain engineering design applications, where understanding uncertainty, chain of action and incorporating domain knowledge and practical experience are so crucial.
Interested in machine learning for engineering? You can find out more here:
#003 - Machine Learning for Civil and Structural Engineers | 01: The Fundamentals
#014 - Machine Learning for Civil and Structural Engineers | 02: Linear Regression
Unlike the deterministic methods prescribed by most design standards, which provide single-point estimates, Bayesian methods yield probability distributions that capture the range of possible outcomes and their likelihood. This probabilistic approach is particularly valuable in infrastructure design, where decisions must balance safety, performance, and cost under uncertain conditions.
For engineers, the practical application of Bayesian methods does not require in-depth knowledge of the underlying mathematics.3
With the right computational tools, Bayesian methods can be easily integrated into the engineering workflow, allowing professionals to focus on the insights these methods provide rather than the complexities of their derivation.
Practical Applications of Bayesian Methods in Infrastructure Design
Bayesian methods are applied across various domains of infrastructure design, providing solutions that enhance decision-making in real-world engineering challenges.
Here are a few examples:
Bridge Design: Fatigue Life Estimation
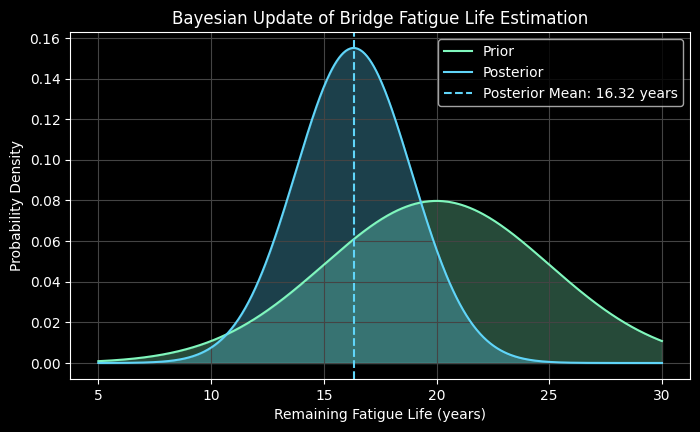
In this example, the Bayesian method is used to update the estimated remaining fatigue life of a bridge based on new inspection data. Initially, we start with a prior estimate of the bridge's fatigue life based on historical data.
Let’s start with a prior estimate that the bridge has 20 years of remaining fatigue life, with a standard deviation of 5 years, reflecting some uncertainty.
New inspection data suggests the fatigue life might be shorter, around 15 years, with a smaller uncertainty of 3 years.
The Bayesian method combines this prior knowledge with the new data to update our estimate. The resulting posterior distribution should reflect a compromise between the prior and the new data, likely showing a remaining fatigue life closer to 16-17 years, depending on the weights of the prior and new data uncertainties.
This process adjusts the initial estimate to account for the latest findings, providing a more accurate assessment of the bridge's condition and guiding maintenance decisions.
Dams and Energy Systems: Predictive Modeling and Risk Assessment
Bayesian methods are particularly useful in the design and management of dams and energy systems, where predictive modeling and risk assessment are essential. For instance, when estimating the energy output of a hydropower facility, engineers might begin with a prior estimate based on historical flow data. As real-time flow measurements and other relevant data become available, this estimate can be updated to provide a more accurate prediction of energy output. Similarly, Bayesian methods can be employed to assess the risk of structural failure due to extreme weather events, enabling proactive management of assets. This approach has been particularly useful in trade-off studies, where I’ve evaluated the timing of repairs or upgrades and considered the impact or likelihood of power interruptions or planned downtime.
Wave-Based Erosion Calculations for Riprap Revetments
Marine structures, such as riprap revetments, are subjected to complex and unpredictable environmental forces, particularly wave-based erosion.
When designing for wave-based erosion for a riprap revetment, you typically start with an initial estimate (or prior) based on historical wind/bathymetric data and your engineering judgment. This might include typical erosion rates based on past observations under similar wave conditions.
However, if you start recording data that shows more erosion than expected, i.e., "excessive erosive action"—this new information changes things.
Bayesian methods are a good option here, you update your model to account for this new data. The result is a new (posterior) estimate that reflects the higher erosion rates.
This updated model might suggest that the current design is more vulnerable to erosion than initially thought, prompting you to consider a more robust riprap material, additional protective measures, or more frequent maintenance checks. Essentially, the model becomes more accurate and better aligned with the actual conditions because it continuously learns and adapts based on the latest data.
Monte Carlo Simulations
Monte Carlo simulations are already widely used in engineering to estimate outcomes and model uncertainties in complex systems. These simulations involve running multiple trials with random inputs to explore the range of possible outcomes. While Monte Carlo simulations are not inherently Bayesian, they are frequently used within the Bayesian framework, particularly for approximating posterior distributions when exact solutions are infeasible.
Monte Carlo simulations are applied to a variety of problems, such as modeling the variability in material strengths, predicting the performance of a dam under different flood/seismic conditions, or assessing the reliability of a bridge under varying loads. By running a large number of simulations, engineers gain a probabilistic understanding of a system's behavior, which helps in assessing risks and making informed decisions.
The utility of Monte Carlo simulations lies in their ability to provide estimates without requiring exact solutions. This makes them a valuable tool for engineers who need to model uncertainties and make informed decisions under conditions of complexity and variability.
Combining them with Bayesian methods make them even more useful.
Practical Example: Using Bayesian Methods to Support Risk-Based Decision-Making
In my sector (Energy and Water), contractors often face decisions about whether to take on a risk or invest in upfront mitigation, they must carefully weigh potential costs against the likelihood of adverse events.
In the case of flood risk during a construction project (e.g. a spillway repair program or a bridge upgrade), Bayesian methods provide a powerful tool to support these decisions by refining risk estimates based on both historical data and newly acquired information.
Scenario:
A contractor is planning a major repair program on a large concrete spillway with a 5-year construction timeline. The site is in a region with some history of flooding. The contractor needs to decide whether to:
Take the risk and proceed without additional flood protection measures, relying on existing infrastructure and standard practices. Essentially, hope for the best.
Invest upfront in mitigation measures, such as temporary flood barriers or enhanced drainage systems, to reduce the risk of flood damage during construction. This snowballs and gets expensive quickly.
Bayesian Analysis:
Initial Risk Assessment (Prior):
The contractor starts with a prior estimate of the annual flood risk, say 2%, based on historical data (a 1-in-50 chance of a significant flood event each year).
New Information (Likelihood):
New environmental assessments or updated climate data suggest that the likelihood of a flood might be higher than the historical average due to recent trends in extreme weather events.
Updated Risk Estimate (Posterior):
Using Bayesian updating, the contractor refines the estimate of the annual flood risk based on this new information. This updated risk is then used to calculate the probability of experiencing at least one flood during the 5-year construction period.
Cost-Benefit Analysis:
Expected Cost Without Mitigation:
\(\text{Expected Cost} = P(\text{flood in 5 years}) \times \text{Cost of Flood Damage} \)This represents the potential cost of taking the risk, calculated by multiplying the probability of a flood by the estimated cost of damages if a flood occurs.
Cost of Mitigation:
\(\text{Cost of Mitigation} = \text{Upfront investment in flood protection}\)This is the fixed cost of implementing mitigation measures to reduce or eliminate flood risk.
Decision Making:
The contractor compares the expected cost of taking the risk with the cost of mitigation. If the expected cost of potential flood damage exceeds the cost of mitigation, it may be more prudent to invest upfront. Conversely, if the likelihood of flooding is sufficiently low, the contractor might decide to accept the risk and avoid the mitigation costs.
Python Example with Cost Analysis:
Here’s how you could extend the previous example to include a simple cost-benefit analysis:
import numpy as np
import scipy.stats as stats
# Prior and posterior setup
prior_flood_prob = 0.02 # Prior probability based on historical data (1 in 50 years)
new_data_mean = 0.04 # Mean probability suggested by new data
new_data_std = 0.02 # Uncertainty in the new data
# Bayesian update: combining prior with new data to form the posterior
posterior_mean = (prior_flood_prob + new_data_mean) / 2 # Averaging prior and new data means
posterior_std = np.sqrt((0.5 * prior_flood_prob)**2 + (0.5 * new_data_std)**2) # Combining uncertainties
# Calculating updated flood probabilities
annual_flood_prob = stats.norm(posterior_mean, posterior_std).mean() # Mean annual flood probability
five_year_flood_risk = 1 - (1 - annual_flood_prob)**5 # Risk of flooding over 5 years
# Cost analysis and decision-making
cost_of_flood_damage = 5000000 # Estimated cost of flood damage in dollars
cost_of_mitigation = 150000 # Cost of implementing flood protection measures in dollars
expected_cost_without_mitigation = five_year_flood_risk * cost_of_flood_damage
# Decision: Compare expected cost without mitigation to mitigation cost
if expected_cost_without_mitigation > cost_of_mitigation:
decision = "Invest in mitigation"
else:
decision = "Take the risk"
# Output results
print(f"Posterior annual flood probability: {annual_flood_prob:.4f}")
print(f"Risk of at least one flood during the 5-year construction period: {five_year_flood_risk:.4f}")
print(f"Expected cost without mitigation: ${expected_cost_without_mitigation:,.2f}")
print(f"Cost of mitigation: ${cost_of_mitigation:,.2f}")
print(f"Decision: {decision}")Output:
Posterior annual flood probability: 0.0300
Risk of at least one flood during the 5-year construction period: 0.1413
Expected cost without mitigation: $706,329.87
Cost of mitigation: $150,000.00
Decision: Invest in mitigation
Explanation:
I assume equal weights for the prior and new data for simplicity, calculating a straightforward average. However, in real-world scenarios, these weights can be adjusted based on the confidence in each data source.
For example, if historical data is highly reliable, it might get more weight, while new, precise data could be prioritized if it's more relevant. This flexibility allows you to tailor the Bayesian update to better reflect the true risk, making your assessment more accurate.
The key mathematical expressions here include:
Posterior Mean: This is calculated by averaging the initial flood probability (from historical data) and the new data's probability. Since we're assuming both are equally reliable, they each contribute equally to the final estimate.
\(posterior\_mean = \frac{prior\_flood\_prob + new\_data\_mean}{2}\)Posterior Standard Deviation: This combines the uncertainties (how unsure we are) from both the prior data and new data. Again, assuming both have equal influence, their uncertainties are combined using a weighted formula.
\(posterior\_std = \sqrt{(0.5 \times prior\_flood\_prob)^2 + (0.5 \times new\_data\_std)^2} \)
This approach simplifies the update by treating both sources of information as equally reliable.
Importance of Data Collection, Organization, and Curation
The effectiveness of Bayesian methods and Monte Carlo simulations hinges on the quality of the data used in the analysis. In infrastructure design, collecting, organizing, and curating high-quality data is essential for making accurate predictions and informed decisions. Data sources may include historical records, sensor data, environmental monitoring, and results from field tests.
Challenges in data management, such as inconsistencies, gaps, or inaccuracies, can undermine the reliability of Bayesian methods. Therefore, we must prioritize robust data collection practices and employ technologies that enhance data accuracy and availability. Proper data curation ensures that the data is relevant, up-to-date, and representative of the conditions being modelled, ultimately leading to more reliable outcomes in Bayesian analysis.
The most critical aspect of designing with data is applying sound engineering judgment. Data should inform decisions, but it must be balanced with real-world experience and the specific goals and constraints of the project.
This approach is vital in infrastructure projects, where high stakes, ambiguous conditions, and narrow margins for error demand precision and reliability.
Conclusion
Bayesian methods are powerful tools that enhance decision-making in infrastructure design. By incorporating prior knowledge and updating predictions as new data becomes available, Bayesian methods offer a practical approach to managing uncertainty in engineering.
For engineers, the focus should be on the practical application of these tools rather than on understanding the deep mathematical foundations.
As these tools become more accessible and user-friendly, their adoption will continue to grow, empowering us to tackle the complex challenges of infrastructure design with more confidence and precision.
If you’re interested in these kinds of hypothetical case studies, let me know. I have a lot more to share on these topics but I’m not sure if I’m screaming into the abyss or not. So far, the statistics indicate engineers are interested in these topics but please drop me a comment or rant and weigh in.
The Flocode Community is steadily growing, reaching engineers in 126 countries. A couple of weeks ago, I almost got a guy from Greenland to join us but then he ghosted me.
Greenland, we’re coming.
Stay safe out there, see you in the next one.
James 🌊
Hon, C. K. H., Sun, C., Xia, B., Jimmieson, N. L., Way, K. A., & Wu, P. P.-Y. (2022). Applications of Bayesian approaches in construction management research: A systematic review. Engineering, Construction and Architectural Management, 29(5), 2153-2182. https://doi.org/10.1108/ECAM-10-2020-0817
Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007. (n.d.). Implementation of Eurocodes: Handbook 2 - Reliability Backgrounds. Guide to the basis of structural reliability and risk engineering related to Eurocodes, supplemented by practical examples. Retrieved from https://eurocodes.jrc.ec.europa.eu/sites/default/files/2021-12/handbook2.pdf
Downey, A. B. (2021). Think Bayes: Bayesian Statistics in Python. O'Reilly Media. Second Edition. https://www.goodreads.com/book/show/58097122-think-bayes
👆 I highly recommend Allen Downey’s books. He is one of the best authors at explaining Python and Data Science Methods.
He also has a great newsletter here: Probably Overthinking It